Unicircles Rank: 11 (0 members)
Your Status:
Login required
Unicircles Rating:
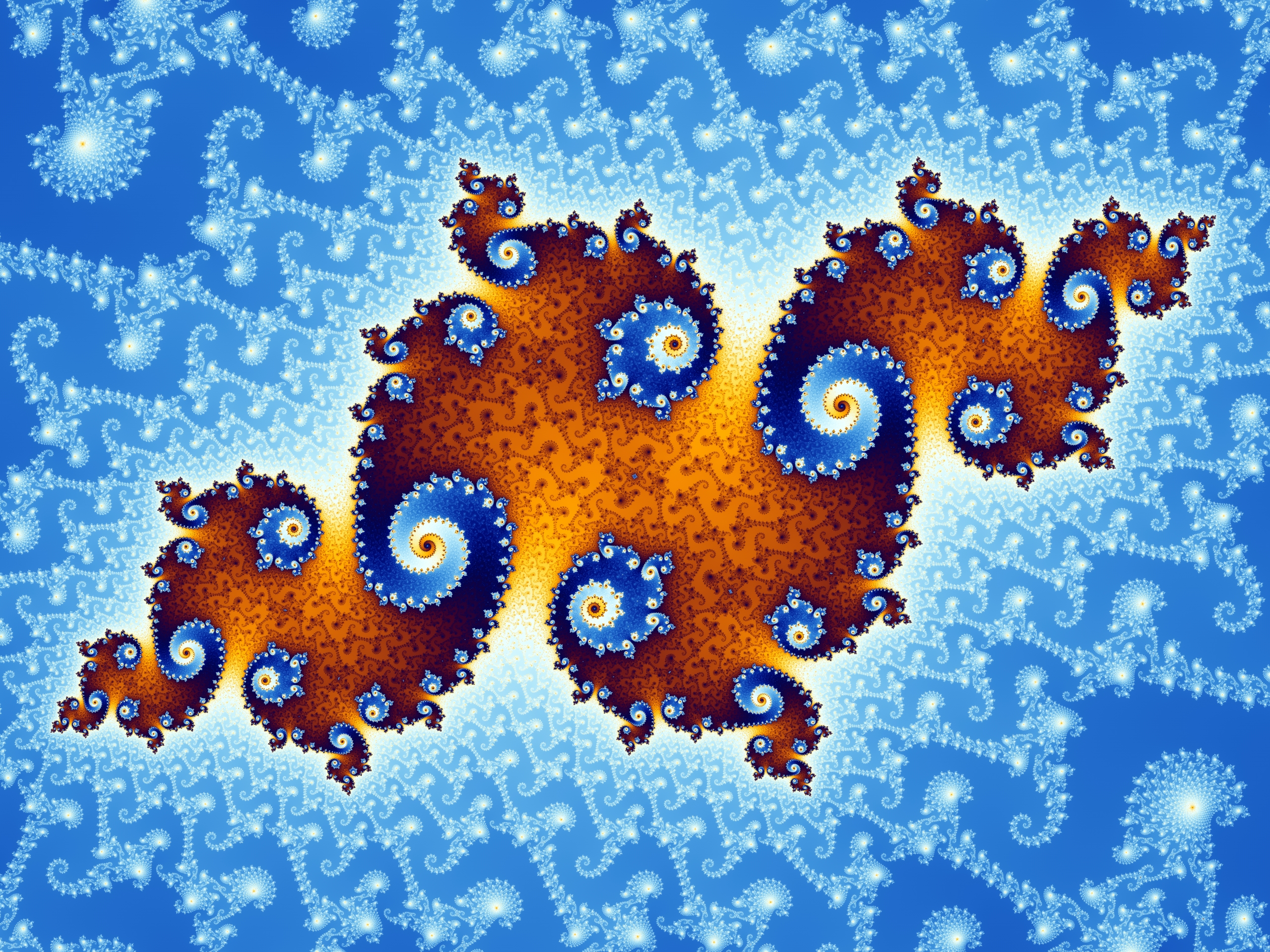
In mathematics, a fractal is a geometric shape containing detailed structure at arbitrarily small scales, usually having a fractal dimension strictly exceeding the topological dimension. Many fractals appear similar at various scales, as illustrated in successive magnifications of the Mandelbrot set. This exhibition of similar patterns at increasingly smaller scales is called self-similarity, also known as expanding symmetry or unfolding symmetry; if this replication is exactly the same at every scale, as in the Menger sponge, the shape is called affine self-similar. Fractal geometry lies within the mathematical branch of measure theory. One way that fractals are different from finite geometric figures is how they scale. Doubling the edge lengths of a filled polygon multiplies its area by four, which is two (the ratio of the new to the old side length) raised to the power of two (the conventional dimension of the filled polygon). Likewise, if the radius of a filled sphere is doubled, i...moreIn mathematics, a fractal is a geometric shape containing detailed structure at arbitrarily small scales, usually having a fractal dimension strictly exceeding the topological dimension. Many fractals appear similar at various scales, as illustrated in successive magnifications of the Mandelbrot set. This exhibition of similar patterns at increasingly smaller scales is called self-similarity, also known as expanding symmetry or unfolding symmetry; if this replication is exactly the same at every scale, as in the Menger sponge, the shape is called affine self-similar. Fractal geometry lies within the mathematical branch of measure theory. One way that fractals are different from finite geometric figures is how they scale. Doubling the edge lengths of a filled polygon multiplies its area by four, which is two (the ratio of the new to the old side length) raised to the power of two (the conventional dimension of the filled polygon). Likewise, if the radius of a filled sphere is doubled, its volume scales by eight, which is two (the ratio of the new to the old radius) to the power of three (the conventional dimension of the filled sphere). However, if a fractal's one-dimensional lengths are all doubled, the spatial content of the fractal scales by a power that is not necessarily an integer and is in general greater than its conventional dimension. This power is called the fractal dimension of the geometric object, to distinguish it from the conventional dimension (which is formally called the topological dimension). Analytically, many fractals are nowhere differentiable. An infinite fractal curve can be conceived of as winding through space differently from an ordinary line ' although it is still topologically 1-dimensional, its fractal dimension indicates that it locally fills space more efficiently than an ordinary line. Starting in the 17th century with notions of recursion, fractals have moved through increasingly rigorous mathematical treatment to the study of continuous but not differentiable functions in the 19th century by the seminal work of Bernard Bolzano, Bernhard Riemann, and Karl Weierstrass, and on to the coining of the word fractal in the 20th century with a subsequent burgeoning of interest in fractals and computer-based modelling in the 20th century. There is some disagreement among mathematicians about how the concept of a fractal should be formally defined. Mandelbrot himself summarized it as "beautiful, damn hard, increasingly useful. That's fractals." More formally, in 1982 Mandelbrot defined fractal as follows: "A fractal is by definition a set for which the Hausdorff'Besicovitch dimension strictly exceeds the topological dimension." Later, seeing this as too restrictive, he simplified and expanded the definition to this: "A fractal is a rough or fragmented geometric shape that can be split into parts, each of which is (at least approximately) a reduced-size copy of the whole." Still later, Mandelbrot proposed "to use fractal without a pedantic definition, to use fractal dimension as a generic term applicable to all the variants". The consensus among mathematicians is that theoretical fractals are infinitely self-similar iterated and detailed mathematical constructs, of which many examples have been formulated and studied. Fractals are not limited to geometric patterns, but can also describe processes in time. Fractal patterns with various degrees of self-similarity have been rendered or studied in visual, physical, and aural media and found in nature, technology, art, and architecture. Fractals are of particular relevance in the field of chaos theory because they show up in the geometric depictions of most chaotic processes (typically either as attractors or as boundaries between basins of attraction)....less
Circles
Research Topics


